The Ionic Lattice
Crystal Packing
In an ionic solid, the ions are packed together into a repeating array called a crystal lattice. The concept of crystal packing assumes that the ions are hard spheres. The easiest way to picture such an array is to arrange one layer of spheres and then place successive layers over it.The simplest arrangement is one in which the spheres in the base are packed side by side. The successive layers of spheres are then added directly over the spheres of the layer below. This type of array is known as simple cubic packing.

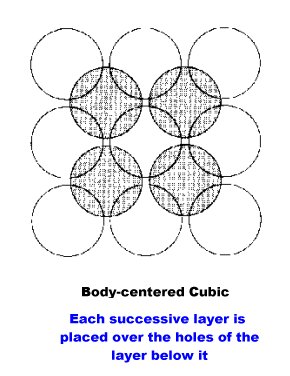
An alternative packing arrangement can be obtained by placing the second layer of spheres over the holes (or interstices) of the base layer. The third layer of spheres are placed over the holes of layer two. Successive layers are added in the same fashion. This type of array is known as body-centered cubic.
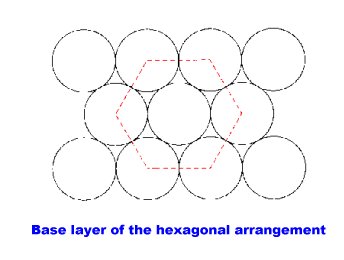
Another arrangement has a base layer of spheres organized in a hexagonal arrangement in which each each sphere is surrounded by six neighbors in the plane.

Each sphere has a coordination number of twelve.
If the third layer of spheres instead of being placed over the hole of the second layer,is placed over the holes not covered from the first layer, the arrangement is called cubic close-packed.
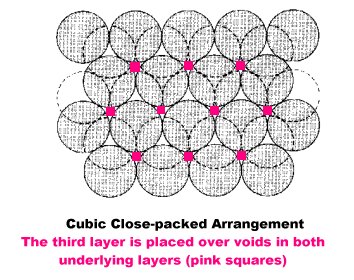
Each sphere has a coordination number of twelve.
Unit Cells
The simplest arrangement of spheres, which will reproduce the entire crystal structure when repeated is called a unit cell. The unit cells for the packing arrangements are shown below.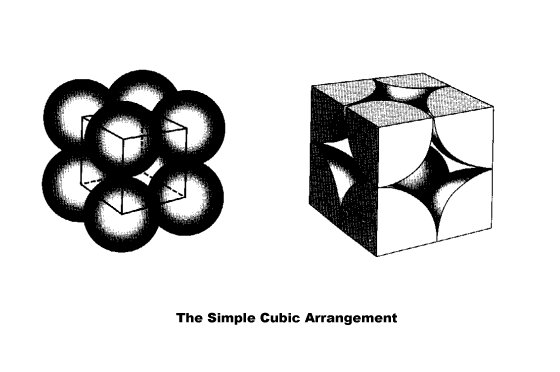
The Ionic Lattice
In most ionic compounds, the anions are much larger than the cations, and it is the anions which form the crystal array. The smaller cations reside in the holes between the anions.Basic Concepts:
- Ions are assumed to be charged, incompressible, nonpolarizable spheres.
- Ions try to surround themselves with as many ions of opposite charge as closely as possible. Usually in the packing arrangement, the cation is just large enough to allow te anions to surround it without touching one another.
- The cation to anion ratio must reflect the stoichiometry of the compound. For MgCl2 the lattice must be an array of chloride anions with only half that number of magnesium ion.
If the cation is too large to give the optimum 0.414 ratio, the anions will be forced apart. When the radius ratio exceeds 0.732, it becomes possible to fit eight anions around the cation. When the ratio is less than 0.414, the anions will be too close together, and the anions will adopt an arrangement that has smaller cavities surrounded by only four anions.
| Radius/Ratio | Preferred Coordination Number | Name |
| Cesium chloride forms a lattice in which the chloride
anions adopt a simple cubic packing arrangement, with each cesium cation occupying the
center of a cube. CsCl has a radius ratio of 0.934 which indicates that the cations
are large enough to prevent the anions from contacting one another. Each unit cell contains
one cesium cation and 8(1/8) chloride ions. Thus, each unit cell contains one formula unit. If the salt does not have a 1:1 stoichiometry, the less common ion occupies a certain proportion of the spaces. In calcium fluoride the cation to anion stoichiometry is 1:2. In the lattice each calcium ion is surrounded by eight chloride ion as in the CsCl lattice. To preserve the 1:2 cation to anion ratio, each alternate interstitial space is empty. This array is termed the fluorite structure. In a compound such as Li2O, the cation to anion ratio is 2:1. The structure is based on the CaF2 lattice, but each alternate anion site is empty. This lattice is named using the prefix anti-. In this case, the array is called an antifluorite structure. |
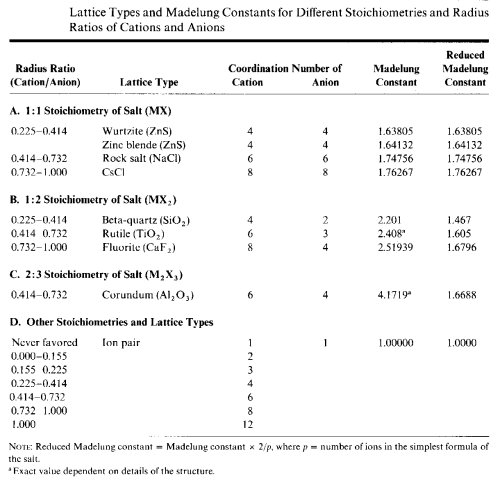
It is possible to predict the coordination number for salts not corresponding to any of the types listed in the table above.
- The radius ratio predicts the coordination number for the less abundant ion in any lattice type and stoichiometry. This is true because the less abundant ions have more neighbors of the opposite charge so crowding is an important issue. Except for compounds such as K2O, the less abundant ion will be the cation. Using the radius ratio values listed in section D of the table, the coordination number of the cation can be predicted.
- The average coordination number of the anion, the more abundant ion, can be determined from the stoichiometry of the salt:
(CN of cation) x (# cations in formula) = (CN of anion) x (# anions in formula)
Anions are usually larger than cations giving a radius ratio less than 1.00. If the ratio is greater than 1.00, the cation is the larger of the two. The salt usually adopts one of the known lattice types with the cation and anion reversing roles in the structure. In these cases, calculate the inverse ratio and add the prefix anti- to the lattice type name.
|
Stability of Lattices and Solubility Rules
Let's compare the lattice energies of thre salts of the same 1:1 stoichiometry (A+X-, B+Y-, C+Z-). Assume the following:- the sum of the cationic and anionic radii, r0, is the same in all three cases
- the average Born exponent is the same in each case
- the radius ratio differs and the first salt has a CsCl structure; the second the NaCl structure; the third the CsCl structure
If you compare the total hydration energy of the cations and anions in each of these salts, you would expect the sum of these energies to be proportional to Z2/r for the cations plus Z2/r for the anion (the Latimethe salt wir equation). The sum of the hydration energies should be most negative for A+X- because it has the most disparate radii. Applying the thermodynamical cycle for solubility, the enthalpy of precipitation should be most positive for A+X- and most negative for C+Z-. The most insoluble salts are typically those in which the hydration energies of the cations and anions are most nearly matched. These are the cations and anions that are most nearly matched in the strength of their acidity and basicity, respectively.
Thus, the ultimate reason that nonacidic cations and nonbasic anions form insoluble salts is that both ions are large (similar in size), forming an especially stable crystal lattice while not giving especially good hydration energies in comparison to the lattice energy.
The reason that acidic cations and nonbasic anions form soluble salts is that the ions are quite different in size giving lower lattice energies than hydration energies.
The difficulty in prediction the solubility of salts of feebly basic anions such as sulfate arises from the fact that these anions are just basic enough to have a -TDS term moderately favoring precipitation with acidic cations while having DH term that is unfavorable due to the anion significantly larger than most acidic cations. Therefore the generalized solubility rule should be modified in the following manner:
large, -2-charged (feebly basic) anions such as sulfate are best precipitated with large, +2-charged (feebly acidic) cations (such as barium).
Smaller, feebly basic anions such as NO2- and ClO2- do not have both the -TDS and DH terms working for insolubility. Salts of these anions tend to be soluble.